【摘要】
通过已知测井资料对油藏储量进行预测,是目前石油行业一个重要的研究课题。文章介绍了一种基于贝叶斯正规化算法的BP神经网络,并把网络应用到油藏参数拟合过程中的具体方法,该方法对提高石油生产效率、降低成本具有很大的作用。
【引言】
油藏参数拟合主要就是非线性函数拟合的过程。非线性函数拟合方法有很多种,主要分为等值线图法、解析内插法、曲面拟合法及神经网络方法等。使用神经网络方法要达到好的拟合效果,主要要解决三个问题:一是样本的选择;二是网络结构的设计;三是训练策略的选择。其中网络结构的设计和训练策略的选择是难点。本文给出的就是基于收敛速度快、泛化能力较强的贝叶斯正规化算法的神经网络进行设计的具体方法。
【正文】
1、油藏参数拟合中需要解决的问题
假定油藏储量与测井资料中的数据存在以下数学模型:
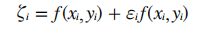
式中,f(xi , yi)为对应输入与输出之间的关系式,fi为误差。现假定:
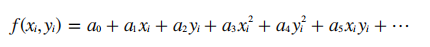
那么,对于每个样本值,都可以列出以上方程,并在∑ε²min=条件下,求解出ai的值,最终求出待求点的油藏储量。
假设区域内有6个公共点。此时有:
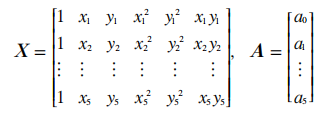
这样,我们需要解决的问题就是按某种方法求出模型待定参数a0a1a2a3a4a5的数值。
2、BP网络与贝叶斯正规化算法
人工神经网络是生物神经系统的一种高度简化后的近似。它具有非线性映射能力和无模型估计的特征,是处理非线性映射问题的有效工具。BP网络是应用最为广泛的神经网络。它具有输入层、输出层、隐含层(一层或多层),相邻层之间通过权值全连接。它包括信息的正向传播和误差的反向传播两个过程,输入时由输入层经中间层向输出层顺向传播;实际输出与期望输出之差值(即误差)由输出层经中间层向输入层逐渐修正连接权的方式逆向传播。两个过程反复交替,就可以使网络趋向收敛。该网络的结构、学习样本与训练策略对网络性能影响很大,为了解决其训练速度慢和易于陷入局部最小值的缺点,设计可以采用Levenberg-Marquardt(LM)算法;为了防止过拟合,设计采取在训练样本中随机添加噪声的方法;为了提高泛化能力,则可采用贝叶斯正规化法来解决。下面介绍实现拟合的具体过程。在介绍之前,下面先介绍一下神经网络的基本知识。
3、神经网络介绍
3.1 人工神经元模型
图1所示是一个人工神经元的基本模型图。
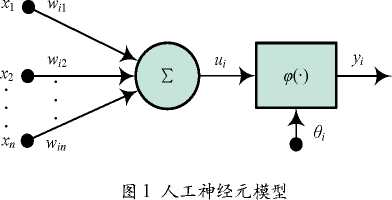
图1中的作用可分别以下面的数学式表达:
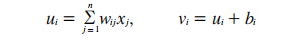
其中,xj(j=l,2,...n)为神经元i的输入信号;为突出强度或连接权;u是由输入信号线性组合后的输出;i为人工神经元的阈值或称偏差(用b,表示);V,为经偏差调整后的值,也称为神经元的局部感应区;{(.)为激励函数;y是神经元i的输出。这样,则有:
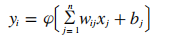
典型的BP神经网络是含有一个隐含层的三层网络结构,其中包括一个输入层,一个输出层,一个隐含层。图2所示是一个三层BP网络结构图。
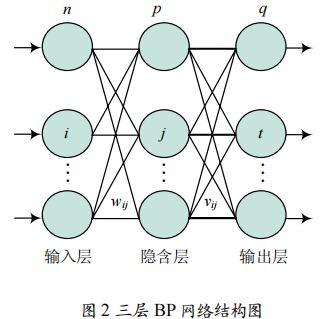
这个网络输入层有n个神经元,输出层有q个神经元,隐含层有p个神经元。输入信号从输入层节点依次传过各隐层节点,然后传到输出层,每一层节点的输出只影响下一层节点的输出,相邻层每个节点通过适当的连接权值向前连接。
3.3 神经网络模型在软件中的设计与实现
采用贝叶斯正规化BP神经网络的三层网络设计模型,应首先确定各层神经元的个数{Var_num,M,1}(Var_num为输入参数的个数,隐藏层神经元个数可通过计算得出);为了计算方便,这里首先把网络变量设置如下:
输入模式向量:Ak=(aik,a2,•••,a:);期望输出向量:Z=3讨,;中间层各单元输入向量:S*=(詩,履,…,sp);中间层各单元输出向量:Bk=(bt,b2,•••,bp);输出层各单元输入向量:Lt=仏将,•,iq);输出实际值向量:Ck=(c"c2,•,c;)。
输入层至中间层的连接权为WiJ;中间层至输出层的连接权为v;中间层各单元的阈值为伤;输出层各单元的阈值为*。其中:
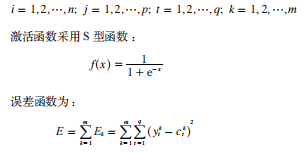
学习算法采用L-M优化算法。L-M算法又称阻尼最小二乘算法,其权值调整公式为:
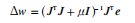
其中,•/为误差对权值微分的雅克比矩阵,e为误差向量,M为阻尼因子,/为单位矩阵。
标准神经网络学习的目的是找出使误差函数E为最小的网络参数W,而使上述目标函数达到最小的函数有无限多个,即式子的解并不唯一。因此,由有限数据点恢复其背后隐含的规律问题往往不太合适,而应采用正规化理论,即加入一个约束性项使问题的解稳定,从而得到有用的解。依据正规化的理论设置的目标函数为:

其中,Ew代表正规化方法中网络的复杂性和平滑性,P代表平滑性约束算子控制着其他参数(权与阈值)的分布形式,被称为超参数。正规化法通过采用新的性能函数,可以在保证网络训练误差尽可能小的情况下,使网络的有效权值尽可能少,从而有利于提高神经网络的泛化能力。超参数a,P的大小决定着网络训练误差和网络结构的复杂性,常规的正规化方法很难确定超参数a,P的大小,所以,应采用贝叶斯方法来确定超参数,可以在网络的训练过程中自适应地调节超参数的大小,使其达到最优。采用贝叶斯方法计算超参数的公式如下:
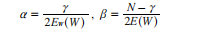
其中,c=N-2atr(A)-1,A是F(w)的Hessian阵,z表示有效的网络参数的数目,可用于反映网络的实际规模,N是网络所有参数的数目。
在软件中实现神经网络模型的步骤如下:
第一步:初始化a、及权值w、%以及阈值i、c,设a=0,b=1,并用Nguyen-Widrow法初始化权值。
第二步:利用L-M算法最小化目标函数Fw=bE+aEw。
首先,应将所有样本归一化值输入到网络并用公式计算出网络输出,再用误差函数计算出训练集中所有目标的误差平方和。计算过程如下:
(1)用输入样本归一化值Ak=(*',ak,•••,an)、连接权Wj及阈值i计算中间层各单元的输入j然后用勇通过传递函数计算中间层各单元的输出:
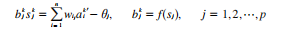
(2)同理计算输出层各单元的输入l,以及输出层单元的响应C:
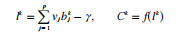
(3)计算训练集中所有目标的误差平方和:
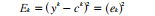
之后,再计算出误差对权值微分的雅可比矩阵。雅可比矩阵元素计算公式如下:
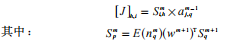
式中,Sm代表误差对m层输入的第i个元素的敏感性,n为每层网络的加权和。
然后再用公式Dw=(尸J+nI尸尸e,求出Dw。最后,用w+Dw重复计算误差平方和。如果新的和小于第一步中计算的和,则用n除以>1),并转入第Q)步;否则,直接用n除以i。当误差平方和减小到某一目标时,算法即被认为收敛。
第三步:计算有效参数的数目c=N_2atr(A)T,其中海森矩阵A利用Gauss-Newton逼近。
第四步:计算目标函数的新参数值。
第五步:迭代进行第二到第四步,直到收敛为止。
在训练过程中,可以根据有效参数c,E,Ew的取值来确定隐藏神经元的个数(记为M)及网络是否收敛。对于给定的M,当经过若干步迭代后,如果这三个参数处于恒值或变化较小,则脱明网络训练收敛,可以停止训练。
4 结语
实验证明,通过采用拉丁超立方抽样方法选取样本后,再通过以上贝叶斯正规化和L-M算法设计神经网络,即可最终达到对油藏历史数据进行辅助拟合之目的。
【文章来源】


