椭圆曲线密码

椭圆曲线密码（Elliptic Curve Cryptosystem），简称ECC，是Neal Koblitz和Victor Miller于1985年提出的。

研究发现，有限域上的椭圆曲线上的一些点构成交换群，而且离散对数问题是难解的。于是在此群上定义EIGamal密码，并称为椭圆曲线密码。是不是有些难以理解？没关系，我们接下来一步一步来了解。

目前，椭圆曲线密码已成为除RSA密码之外呼声最高的公钥密码之一，也是目前被广泛使用的最强大的，同时也是最难懂的一个密码学。它密钥短、签名短、软件实现规模小、硬件实现电路省电。普遍认为，160位长的椭圆曲线密码的安全性相当于1024位的RSA密码，而且运算速度也较快。

在ECC流行之前，几乎所有的公钥算法都是基于RSA、DSA和DH等基于模块化算法的可替代的密码系统。RSA和它的朋友在今天仍然非常重要，并且经常和ECC一起使用。

什么是非对称加密（RSA）？

为什么要在这里提到非对称加密呢？因为椭圆曲线加密算法也是基于RSA的，在开始介绍椭圆曲线加密之前，对整个非对称加密有一个概念会对加密算法的理解更有帮助。

非对称加密涉及两个重要概念：公钥（publickey）和私钥（privatekey），公钥公开，私钥保密。

公钥与私钥是一对，如果用公钥对数据进行加密，只有用对应的私钥才能解密；如果用私钥对数据进行加密，那么只有用对应的公钥才能解密。因为加密和解密使用的是两个不同的密钥，所以这种算法叫做非对称加密算法。

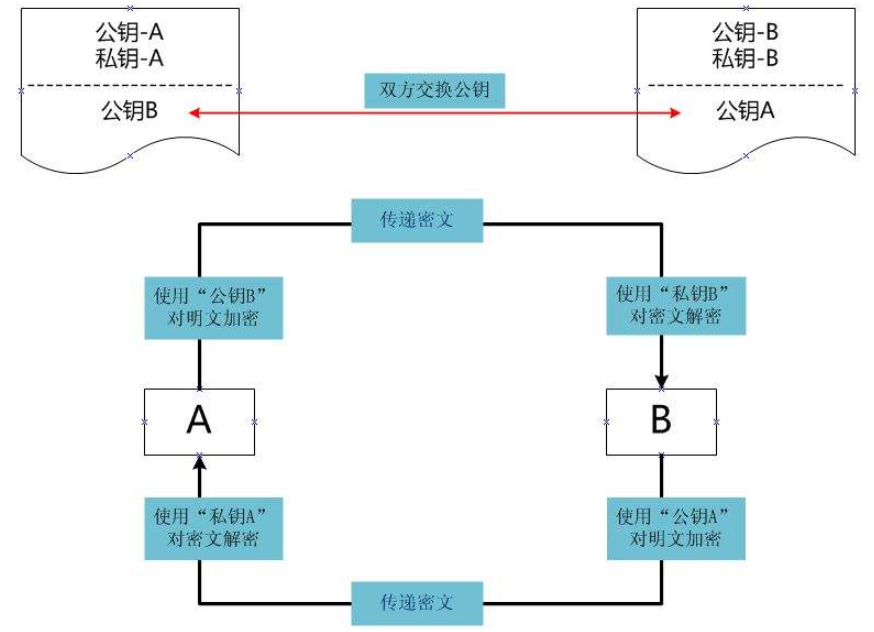
假设现在有A、B双方，A需要向B发送一段信息，整个过程如下：

（1）首先，A和B双方交换公钥，A获得B的公钥（公钥B），B获得A的公钥（公钥A）。

（2）A准备好要传送的明文信息。

（3）A使用“公钥B”对明文进行加密得到密文，然后将密文发送给B。

（4）B用自己的私钥（SK）对密文进行解密得到明文信息。

简单来说，假如说我有一对公钥（PK）和私钥（SK），公钥可以对任何人开放，理论上来说，只要加密算法安全，所有人拿到我的公钥进行加密的密文，只有我自己使用我的私钥才能解密。

再以银行存钱举例来说，假设每个人的密码都不相同，这样每个账号和密码可以组成一队公钥和私钥。我的账号（公钥）可以给任何人，但是我的密码（私钥）只有我自己知道。所有知道我账号的人都可以往我的账号汇钱，但是只有我自己才能从我的账号取钱。

什么是椭圆曲线？

椭圆曲线有多种表示形式，最常见的形式是：

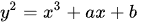
这个式子被称为维尔斯特拉斯通用式。为了让椭圆曲线没有奇异点，即处处光滑可导，需要满足其判别式不为零，即 ：

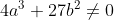
我们来看，下图是满足上式的合法椭圆曲线：

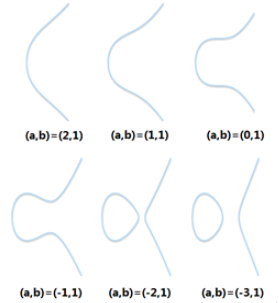
下图是两种非法的椭圆曲线，分别存在一个尖点和叉点使曲线不平滑。

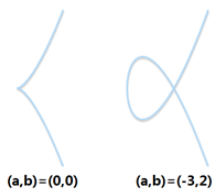
GF(p)上的椭圆曲线

设p是大于3的素数，且4a³+27b²≠0(mod p)，称曲线y²=x³+ax+b（a,b∈GF(p)）为GF(p)上的椭圆曲线。

由椭圆曲线方程可得到一同余方程：y²=x³+ax+b(mod p)（a,b∈GF(p)）

其解为一个二元组(x,y)，其中x,y∈GF(p)，表示椭圆曲线上的一个点，称为该椭圆曲线上的解点。

二次剩余

定理：设m是正整数，a是整数。若同余方程

有解，则称a是模m的平方剩余（或二次剩余）；若无解，则称a是模m的二次非剩余。

为了更方便理解，上式可变化为：x²-a=n*m。其中，n表示m的整数倍

例1：1是模4平方剩余，-1是模4平方非剩余。

详解：令a=1，m=4，x²-1=4*n，可得x=3使得等式成立（此时n=2），即同余方程有解，故1是模4的平方剩余；同理，令a=-1，m=4，x²+1=4*n，此时同余方程无解，故-1是模4平方非剩余。

例2：1、2、4是模7的平方剩余，3、5、6是模7平方非剩余。

例3：直接计算1²，2²，…，14²的模15的平方剩余和平方非剩余。

详解：以1²为例，1²-a=15n，得a=1，即1是模15得平方剩余；以2²为例，2²-a=15n，此时a无解，故2是模15得平方非剩余。

依此类推，得平方剩余为：1，4，6，9，10，平方非剩余为：2，3，5，7，8，11，12，13，14

参考资料

1、椭圆曲线加密概览 - 知乎 (zhihu.com)

2、GF(p)上的ELGamal型椭圆曲线密码详解（Java实现） - 蒙丿鑫 - 博客园 (cnblogs.com)